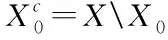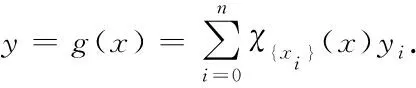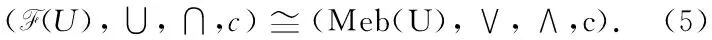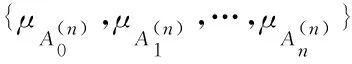李洪兴
(1. 北京师范大学珠海校区 应用数学与交叉科学研究中心, 广东 珠海 519085; 2. 大连理工大学 控制科学与工程学院, 辽宁 大连 116024)

为了说明问题的实质,当取U=R时,那么这个函数可以看作一个单位脉冲波,见图1.

图 1 单位脉冲波
特别地,当A=[a,b]⊂R时,这个函数可以视为一个单位矩形波,见图2.

图 2 单位矩形波


(A,B)→A∪B=∪(A,B)=
{u∈U|(u∈A)∨(u∈B)};

(A,B)→A∩B=∩(A,B)=
{u∈U|(u∈A)∧(u∈B)};

A→Ac=c(A)=UA=
{u∈U|u∉A}.
χA∪B(u)=χA(u)∨χB(u), ∀u∈U;
χA∩B(u)=χA(u)∧χB(u), ∀u∈U;
χAc(u)=1-χA(u), ∀u∈U,
其中,∨=max,∧=min,即
a∨b=max{a,b}, ∀a,b∈R,
a∧b=min{a,b}, ∀a,b∈R.

A×B:={(a,b)|a∈A,b∈B}
叫做A与B的直积.特别地,有
U×V={(u,v)|u∈U,v∈V}.
不难验证结果
χA×B(u,v)=χA(u)∧χB(v)=
χA(u)·χB(v), ∀(u,v)∈U×V.
现在引入符号
Ch(U)={χ|χ:U→[0,1]},
在集合Ch(U)上定义2个二元代数运算∨、∧和一个一元代数运算“c”如下:
∨:Ch(U)×Ch(U)→Ch(U),
(χ1,χ2)→χ1∨χ2=∨(χ1,χ2),
(χ1∨χ2)(u)=χ1(u)∨χ2(u), ∀u∈U;
∧:Ch(U)×Ch(U)→Ch(U),
(χ1,χ2)→χ1∧χ2=∧(χ1,χ2),
(χ1∧χ2)(u)=χ1(u)∧χ2(u), ∀u∈U;
c:Ch(U)→Ch(U),χ→χc=c(χ),
χc(u)=1-χ(u), ∀u∈U.
这样就构成一个代数系统(Ch(U),∨,∧,c).


不防证明(1)式.事实上,考虑映射


[(u∈A)∧(u∉B)]∨
[(u∉A)∧(u∈B)]
为真.无妨假定(u∈A)∧(u∉B)为真,那么有
(χA(u)=1)∧(χB(u)=0),

A={u∈U|χ(u)=1}.
根据这个集合A,又可以得到一个函数χA∈Ch(U)如下:
χA:U→{0,1},

接下来,证明χA=χ.实际上,对于任意的元素u∈U,显然有
χA(u)=1⟺u∈A⟺χ(u)=1.
由此可见χA=χ,即
f(A)=χA=χ,
所以f是个满射,从而f是双射.
f(A∪B)=χA∪B,
f(A∩B)=χA∩B,
f(Ac)=χAc.
只需观察下面的事实:对于任意的元素u∈U,有:
[f(A∪B)](u)=χA∪B(u)=
χA(u)∨χB(u)=
[f(A)](u)∨[f(B)](u)=
{[f(A)]∨[f(B)]}(u),
[f(A∩B)](u)=χA∩B(u)=
χA(u)∧χB(u)=
[f(A)](u)∧[f(B)](u)=
{[f(A)]∧[f(B)]}(u),
[f(Ac)](u)=χAc(u)=1-χA(u)=
1-[f(A)](u)=[f(A)]c(u).
可见双射f确实保持代数运算,从而f是个同构映射.
因为

所以论域U中的一个集合就是定义在U上的一个波函数,反之亦然;这就叫做波集二象性.



(2)
事实上,对于任意的u∈U有
χA(u)=1⟺u∈A⟺
1+0=1.
这种情况足以启发产生一种新的思想:在实际的宏观物理世界,任何一个物体可以视为一个质点,而该物体一定由大量的微观粒子所构成.如果宏观质点运动也具有波动性,而微观粒子运动是具有波粒二象性的,那么宏观质点运动的波函数一定是有若干微观粒子运动的波函数构成.可喜的是,文献[1]已经证明了宏观质点运动也具有波动性,换言之,宏观质点运动是具有波质二象性的.
从一类具有单输入单输出的开环系统谈起,见图3,其中S代表一个系统,x表示在论域
X=[a,b]⊂R
中取值的输入变量,y表示在论域
Y=[c,d]⊂R
中取值的输出变量.

图 3 单输入单输出的开环系统
如果S是一个复杂的不确定系统,那么对这个系统采用常规的机制建模法是困难的,甚至是不可能的.对于这种情况,可以通过实验来得到一组离散的数据,由它近似地表示该系统的输入输出关系[2].这组数据用符号IOD来表达如下
IOD≜{(xi,yi)|i=0,1,…,n}⊂X×Y,
这里的输入数据和输出数据可以分别表示为:
X0≜{xi|i=0,1,…,n},
Y0≜{yi|i=0,1,…,n},

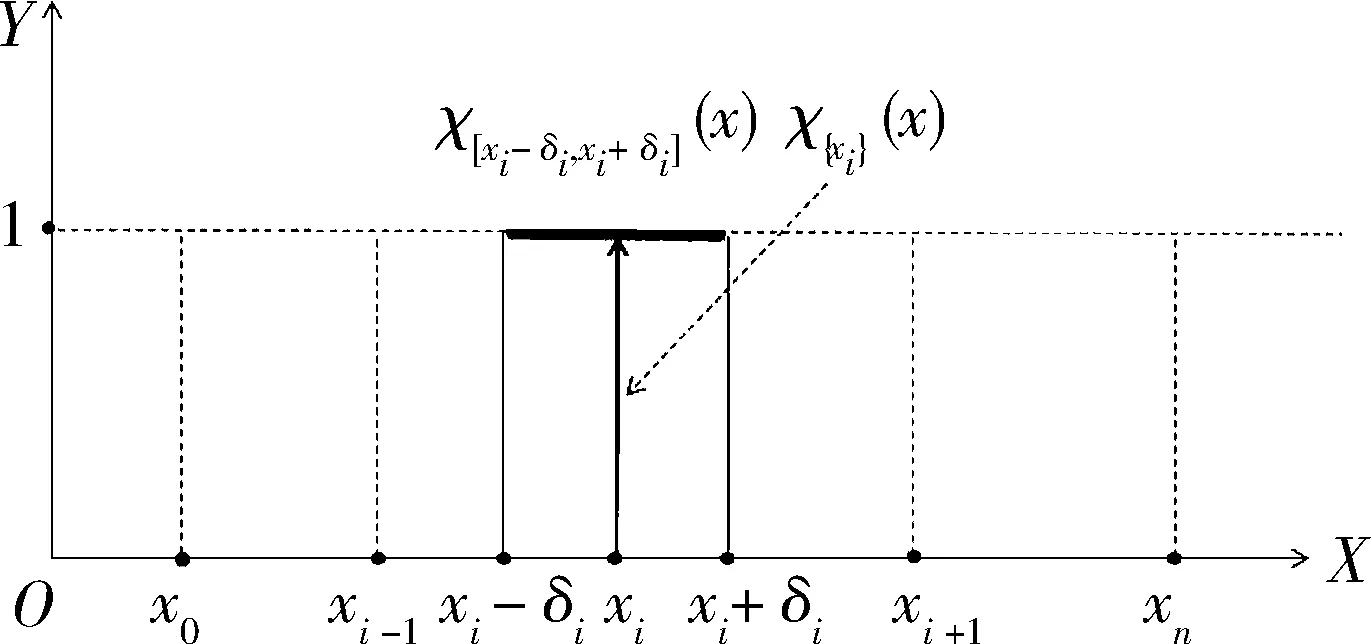
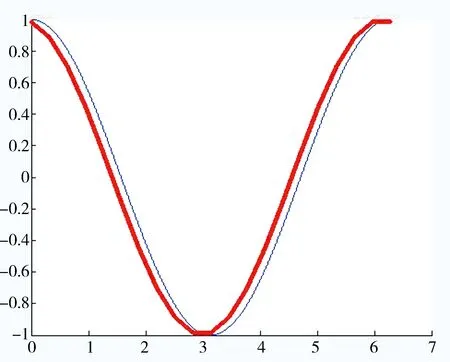
a=x0 实际上,IOD可以看作一个离散的函数 g0:X0→Y0,xi→g(xi)≜yi, i=0,1,…,n. 图 4 系统的离散响应 现在扩展函数g0:X0→Y0的定义如下: g:X→Y, 尽管映射g:X→Y使得系统S对于每一个x∈X都有响应,即 i=0,1,…,n. 如果注意到g(x)=0(∀x∈XX0),可见系统S在XX0中的响应几乎无意义. 于是应该思考一个问题:如何利用已知的映射g0:X0→Y0来构造一个实用的映射f:X→Y使得系统S对于X中的每一个元素都具有实用价值的响应,并且满足如下的自然条件: f(xi)=g0(xi), ∀i∈{0,1,…,n}. 当然,众所周知,插值是解决这个问题的一个方法;不过插值方法不具有系统的观念,也不具有集合运算、逻辑和推理的意义[3].下面将采用集合、逻辑和推理的思想来解决该问题. 首先,不难理解,通过实验得到的数据xi、yi,i=0,1,…,n都具有误差,于是便有下面的表达式: xi±δi,yi±εi,δi≥0,εi≥0, i=0,1,…,n, 或者可以写为下列集合形式(区间是集合): xi∈[xi-δi,xi+δi], yi∈[yi-εi,yi+εi], i=0,1,…,n. 这意味着数据被一步步扩展为下面的集合形式[4]: IOD={(xi,yi)|i=0,1,…,n}⟹ {({xi},{yi})|i=0,1,…,n}⟹ {([xi-δi,xi+δi],[yi-εi,yi+εi])| i=0,1,…,n}. 注意每个误差区间的特征函数形式: χ[xi-δi,xi+δi](x)= i=0,1,…,n. 基于上面讨论的波集二象性,每个单位脉冲波χ{xi}(x)扩展为单位矩形波χ[xi-δi,xi+δi](x),见图5. 图 5 单位脉冲波到单位矩形波 从单位脉冲波χ{xi}(x)到单位矩形波χ[xi-δi,xi+δi](x),实际上利用数据的误差获得了更多的信息.现在计算来自误差区间[xi-δi,xi+δi]的一种类型的信息量如下 (3) 如图6所示,系统在位于一些间隔(interspaces)上的输入量也是没有响应的. 图 6 系统在间隔上没有响应 为了解决这个问题,思想是在保持信息量不变的情况下,考虑使用另外一些形式的波函数μAi(x),当然它们也是某种类型的集合Ai的波函数,见图7. 所谓保持信息量不变,就是要求满足条件 图 7 作为某种集合Ai的波函数μAi(x) 如果取下面形式的2个数: 那么就可以得到如下的波函数: 不难验证,上述形式的波函数已经满足条件: 同时不难知道这些波函数适合下面的条件: μAi(X)=[0,1], ∀i∈{0,1,…,n}, 这里μAi(X)是函数μAi关于论域X的象集,它们不同于χ[xi-δi,xi+δi](X)={0,1}.因此,从波函数的角度讲,是对集合形式的一种推广. 基于前面讲过的波集二象性,可以猜测或想象,波函数μAi(x)应该对应一种新的集合形式,称之为“Fuzzy集合”. 回顾上一节的事实 μAi(X)=[0,1], ∀i∈{0,1,…,n}, 自然会给出定义:所谓论域U上的一个Fuzzy集A是指,对于任何元素u∈U,存在唯一的一个实数μA(u)∈[0,1]与u对应,这里μA(u)叫做元素u关于A的隶属度.这意味着得到一个映射 μA:U→[0,1],u→μA(u), 类似于描述集合的Venn图,可以给出描述Fuzzy集的泛Venn图.事实上,首先用一个矩形表示论域U.然后,论域U中的元素用具有单位长度的线段来表示,而论域U上的一个Fuzzy集A表示为矩形中的一个椭圆,见图8,可见: μA(u1)=1,μA(u2)=0, μA(u3)=0.3,μA(u4)=0.6. 图 8 泛Venn图 μA(U)={0,1}, 则隶属函数便退化为特征函数,这意味着: A={u∈U|μA(u)=1}. 因此,Cantor集合是Fuzzy集合的特例[6].注意到 μA(u0)∈(0,1), ∃u0∈U, 这里(0,1)是个开区间.(4)式所表达的Fuzzy集 μAi(x),i=0,1,…,n, 就是常用的真Fuzzy集的例子. 回顾代数系统(Ch(U),∨,∧,c),记 Meb(U)={μ|μ:U→[0,1]}, 定义2个二元代数运算∨、∧和一个一元代数运算“c”如下: ∨:Meb(U)×Meb(U)→Meb(U), (μ1,μ2)→μ1∨μ2=∨(μ1,μ2), (μ1∨μ2)(u)=μ1(u)∨μ2(u), ∀u∈U; ∧:Meb(U)×Meb(U)→Meb(U), (μ1,μ2)→μ1∧μ2=∧(μ1,μ2), (μ1∧μ2)(u)=μ1(u)∧μ2(u), ∀u∈U; c:Meb(U)→Meb(U),μ→μc=c(μ), μc(u)=1-μ(u), ∀u∈U, 于是便得到一个代数系统(Meb(U),∨,∧,c)[7]. 值得指出的是,从同构关系 A⊃B⟺(∀u∈U)(μA(u)≥μB(u)); A=B⟺(A⊃B)∧(B⊃A)⟺ (∀u∈U)(μA(u)=μB(u)); C=A∪B⟺ (∀u∈U)(μC(u)=μA(u)∨μB(u)); C=A∩B⟺ (∀u∈U)(μC(u)=μA(u)∧μB(u)); C=Ac⟺(∀u∈U)(μC(u)=1-μA(u)). (6) 其实,(6)式也可以写为:∀(u,v)∈U×V,μA×B(u,v)=μA(u)·μB(v). (7) 正是基于同构关系 现在再探讨一下Zadeh的扩展原理.设X和Y为2个非空论域,考虑映射: f:X→Y,x→y=f(x). Zadeh的扩展原理描述的事情是,如何把映射f:X→Y扩展为如下的映射: 首先,考虑Zadeh的扩展原理的特殊情况,即如何把映射f:X→Y扩展为如下的映射: 如图9所示,熟知,映射f实际上是一个关系f⊂X×Y.做下面的集变换: A→B=f°(A)=[(A×Y)∩f]Y. (8) 图 9 Cantor集的集变换 注意,有关Cantor集合与Fuzzy集合的投影以及集变换的具体内容可参考文献[1]中的第二章.特别地,利用文献[1]中的Proposition 2.5.1,有下面的命题. 命题 3.1关于集变换(8)式,有 (9) 证明对于任意的y∈Y,根据文献[1]中的Proposition 2.5.1,有下面的结果: χB(y)=χf°(A)(y)=χ[(A×Y)∩f]Y(y)= 因此,(9)式为真,参见图9. 现在转而考虑如何将映射f:X→Y扩展为下面的映射 从图9得到启发,可以做出如下的Fuzzy集合的集变换: A→B=f*(A)=[(A×Y)∩f]Y. (10) 再利用文献[1]中的Proposition 2.6.1,有下面的命题. 命题 3.2关于Fuzzy集变换(10),有 (11) 证明对于任意的y∈Y,根据文献[1]中的Proposition 2.6.1,有下面的表达式 μB(y)=μf*(A)(y)=μ[(A×Y)∩f]Y(y)= 因此,(10)式为真. 注 3.1表达式(10)恰好是熟知的Zadeh的扩展原理.因为Zadeh的扩展原理是作为原理出现的,故它不需要证明.正如上面的讨论,Zadeh的扩展原理不是个原理,而是个命题,这说明在前面给出的扩展原理是更为基础的原理,使用范围更广,它把Zadeh的扩展原理作为一个命题证明出来,这是很有意义的事情. (10)式是关于一元函数的扩展形式,当然可以考虑多元函数的扩展形式,以二元函数为例进行讨论. 设X、Y、Z是3个非空论域,考虑下面的映射: f:X×Y→Z, (x,y)→z=f(x,y). 首先把映射f:X×Y→Z扩展为下面的样子: 根据文献[1]中的Definition 2.6.1,得到下面的Fuzzy集变换的形式: R→C=f*(R)=[(R×Z)∩f]Z. (12) 然后,利用文献[1]中的Proposition 2.6.1,有下面的命题. 命题 3.3关于Fuzzy集变换(12),有下面的表达式 (13) 证明对于任意的z∈Z,文献[1]中的Proposition 2.6.1,注意事实f⊂X×Y×Z,有下面的结果: μC(z)=μf*(R)(z)=μ[(R×Z)∩f]Z(z)= χf(x,y,f(x,y)))= 便有如下的表达式 因此,(13)式为真. 再继续考虑把映射f:X×Y→Z扩展为下面的样子: (A,B)→C=f*(A,B). (A,B)→C=f*(A,B)= [((A×B)×Z)∩f]Z. (14) 根据文献[1]中的Proposition 2.10.2,对于任意的z∈Z,有下面的结果 (15) 注 3.2关于Fuzzy关系 对于任何的(x,y)∈X×Y,不难知道下面的事实 μR(x,y)=μA×B(x,y)=μA(x)·μB(y). 因此,(15)式也可以写为下面的样子 z∈Z. (16) 还可以考虑另外一个问题.设X和Y是2个非空论域,考虑映射: f:X→Y,x→y=f(x). 熟知,Zadeh的扩展原理是基于映射f:X→Y获得下面的映射: 另一方面,基于映射f:X→Y,应当还考虑如下的逆映射: 为了解作为Fuzzy集合(f-1)*(B)的隶属函数,先考虑特例:把映射f:X→Y扩展为如下的逆映射: 事实上,首先显然有 (f-1)°(B)={x∈X|f(x)∈B}, 于是便有下面的表达式 χ(f-1)°(B)(x)=χ{x∈X|f(x)∈B}(x), ∀x∈X. 命题 3.4∀x∈X,一定有 χ{x∈X|f(x)∈B}(x)=χB(f(x)). 证明对于任意的x∈X,不难看出如下的等价式 χ{t∈X|f(t)∈B}(x)=1⟺ x∈{t∈X|f(t)∈B}⟺ f(x)∈B⟺χB(f(x))=1. 因此,该命题为真. 根据命题3.4,利用提出的扩展原理,可以得到下面的结果 μ(f-1)*(B)(x)=μB(f(x)), ∀x∈X. (17) 这里 n=1,2,3,… 显然它们满足条件 并且 n>m⟹‖Δ(n)‖<‖Δ(m)‖, ∀n,m∈N. 注意到 由此构造如下波函数组(参见图10): i=1,2,…,n-1, 图 10 连续波函数 从而得到一个线性子空间序列 利用f构造常数 由此得到基底一个线性组合 这意味着获得一个连续函数序列 可以验证 图 11 分段线性插值函数 现在仍然使用基函数组 再利用已知的常数组 构造一组新的常数: ∀ε>0, ∃N∈N+, ∀n,m∈N+,n,m>N⟹ 例 4.1导函数逼近的仿真.取 f(x)=sin(x)∈C[0,2π], 熟知 f′(x)=cos(x)∈C[0,2π]. 图12~15是n取不同值时的近似导函数(粗线)和真实导函数(细线). 下面讨论原函数的逼近意义.设函数g(x)∈R[a,b],考虑[a,b]的等距分割全体: 图 12 n=20 图 13 n=40 图 14 n=50 图15 n=100 n=1,2,3,… 利用常数 构造线性方程组 这里 是待求的未知量.写为递推式: … i=1,2,…,n-1, 不难理解,函数g(x)的原函数的一般形式,即原函数的通解为f(x,C0)+C,其中C为任意常数. 例 5.1原函数逼近的仿真.取 g(x)=cos(x)∈C[0,2π], 熟知原函数为 f(x)=sin(x)+C. 取C=0,则 f(x)=sin(x)∈C[0,2π]. 图16~19是n取不同值时的近似原函数(粗线)和真实原函数(细线)的图像. 图 16 n=50 图 17 n=100 图 18 n=200 图 19 n=300