基于改进贝叶斯的重型数控机床可靠性研究

陈红霞，张俊峰*，马爱博，李宏悦，李晨光

(1. 内蒙古工业大学机械工程学院 呼和浩特 010051；
2. 内蒙古自治区先进制造技术重点实验室 呼和浩特 010051)

重型数控机床对现代军工、航天、船舶、轨道交通、发电设备等重工业发展有重要意义[1]。目前，研究人员大多借鉴中小型数控机床的可靠性模型对重型数控机床进行可靠性分析[2]。重型数控机床具有加工工况复杂、故障溯源困难、维护成本较高、故障样本数据匮乏等特点，这对重型数控机床的可靠性评估及后续研究都造成极大困难[3]。小样本数据下的重型机床可靠性评估，是目前可靠性研究的一个难题[4]。

数控机床的可靠性研究最早开始于20 世纪70 年代[5]，前苏联专家对建立机床参数模型和机床工艺可靠性方面进行了相关研究[6]。近些年来，一些专家将贝叶斯理论引入小样本条件下的重型数控机床可靠性建模[7]，根据先验信息和主观经验进行模型参数估计[8]。文献[9]采用威布尔双参数和三参数分布对重型数控机床零部件或系统建模[9]。文献[10]采用极大似然估计法和Edgeworth 级数法对重型数控机床的故障模型进行参数估计，并解释参数估计结果与数据拟合的关系。文献[11]利用第二类极大似然方法得到折合因子的贝叶斯估计[11]。文献[12]在马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)方法的基础上针对数据的多源性，建立多源异种数据融合模型，为小样本的可靠性建模提供新思路。上述研究对小样本数据下的可靠性建模问题提出了不同的方法，给重型数控机床可靠性建模及评估奠定了理论基础。

本文基于改进的贝叶斯方法对重型数控机床进行可靠性建模与评估。首先，选取双参数的威布尔分布对机床故障数据进行拟合，采用极大似然参数估计法和贝叶斯参数估计法对可靠性模型求解。其次，对传统的贝叶斯估计法进行改进，得到分层贝叶斯模型，通过对比分析及仿真实验，证明改进后的贝叶斯模型在小样本数据条件下更具有优越性。最后，利用分层贝叶斯模型对该机床进行可靠性评估，得到其理论故障间隔时间。

1.1 传统可靠性模型

一般地，对系统建立可靠性模型均采用双参数威布尔分布。以重型数控机床故障间隔时间为参数，经过变换得到服从威布尔分布的可靠性模型。此时，机床可靠性服从威布尔分布的概率密度函数和概率分布函数分别为：

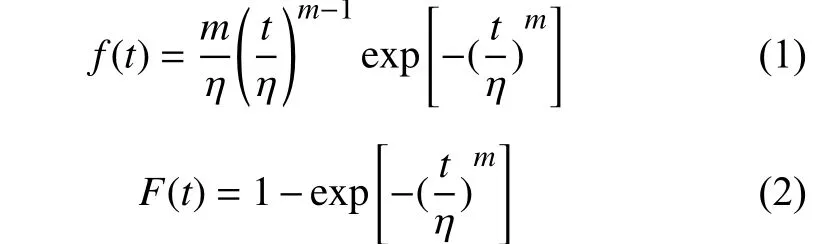
式中，m和η 分别为威布尔分布的形状参数和尺度参数；
t为机床的故障时间。

1.2 极大似然估计法

一般地，采用极大似然估计对分布函数进行参数估计。当已知分布模型中有未知参数θ1,θ2,···,θk时，可以建立似然函数表达式：

式中，ti为实际采集的数据子样(i=1, 2, ···,n)。

在威布尔分布模型中，未知参数为m和η，将式(1)的威布尔分布概率密度函数代入式(3)中，建立的极大似然函数为：

1.3 基于贝叶斯理论的参数估计

由贝叶斯参数估计理论可知，在对分布函数的参数估计中，所有未知参数都被认为是随机变量。求解待估参数值时，需要先根据观测数据和主观经验设定其模型的先验分布，进而求出参数估计结果。其中，先验分布的选择优劣会直接影响模型参数估计的精度。

基于贝叶斯理论对重型数控机床建立可靠性模型，具体思路为在研究对象样本数据和先验信息的基础上，建立其贝叶斯模型，计算模型参数的后验分布并得出相应的概率分布。

结合贝叶斯定理分析可知，分布模型参数的后验分布可以表示为：

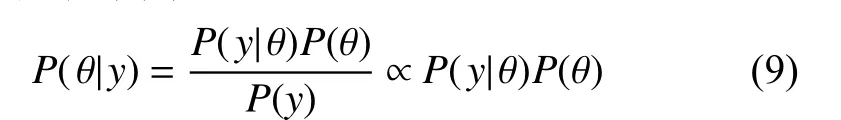
式中，θ 为待估计的参数；
y为基于观测数据的信息；
P(θ)为 参 数 θ 的先验 概 率；
P(y|θ)是设定 参 数θ 条件下的数据所服从的后验分布；
P(y|θ)/P(y)为事件y对参数设定的支持程度，即似然函数。

因为正态分布是威布尔分布的共轭先验分布模型，所以设定威布尔分布的参数m和η 服从正态分布，这里用N来表示。

经过推导，得到重型机床基于贝叶斯理论的可靠性模型，如式(10)所示：

1.4 层次贝叶斯模型

为了优化贝叶斯参数估计的方法，将待估参数的先验分布进一步分化，得到层次贝叶斯模型。层次贝叶斯模型理论上可以分为N层，但随着分化层数的增加，模型的计算效率逐渐降低。为了保证计算效率，采用两层贝叶斯模型进行分析。

由一般贝叶斯模型可知，m～N(α1,β1)为参数m的先验分布， η～N(α2,β2) 为 参数 η的先验分布。将α2～unif(α1′,β1′),β2～unif(α2′,β2′)分别作为参数m, η 的先验分布，这样就得到了更进一层的贝叶斯模型，这里称 α2,β2为超参数，unif 表示均匀分布，表达如下：

经过上式推导，即可得到基于层次贝叶斯理论的可靠性模型。

1.5 贝叶斯模型的求解方法

求解贝叶斯模型的参数需要计算高维积分的边缘后验分布，而且随着模型组成的复杂会使参数求解变得更加困难。通过引入 MCMC 方法对模型进行数据模拟、迭代以提升参数求解的效率。该方法中包含多种抽样方法，包括Metropolis-Hastings 抽样方法和 Gibbs 抽样方法。其中，Metropolis-Hastings抽样方法更为高效，具体操作流程如图1 所示。

图1 蒙特卡洛仿真流程

通过MCMC 法处理得到模型待估参数的后验分布，取其期望值作为参数估计的结果，基于排序取分位数法，可以求出待估参数的置信区间。

1.6 参数估计结果分析

为了分析参数估计结果的优劣，本文采用统计学中的均方根误差值(normalized root mean square error, NRMSE)，NRMSE 值越小则结果精度更优。计算方法为：

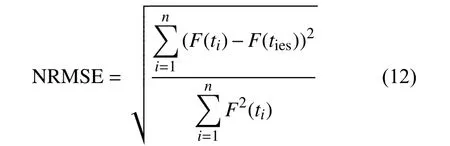
式中：F(ti)是机床的累计故障概率，F(ties)是将参数估计值代入累积故障概率函数后所得到的累积故障概率值。

重型机床故障数据样本量较小、数据跨度较大、故障发生具有不确定性，若采用一般统计学方法无法对此类问题进行有效分析，本文基于贝叶斯理论进行分析，可以一定程度优化分析结果。

2.1 故障数据预处理

本文采集某企业近3 年内，某型号重型数控机床的停机维修记录共58 条。通过数据预处理，得到该机床的故障间隔时间，其中部分结果为22 h，23 h，24 h，···，912 h，936 h，1 248 h。

2.2 参数估计结果

将故障间隔时间代入机床的双参数威布尔分布可靠性模型中，利用最大似然参数估计法和贝叶斯参数估计法分别对分布模型的参数进行求解。采用最大似然参数估计法得到的结果如表1 所示，用下标MLE 来表示。

表1 最大似然参数估计结果

将机床的故障间隔时间从大到小排列，代入式(13)所示的中位秩公式：

计算该重型机床实际的累计失效概率密度，得到其点位分布图，如图2 所示。

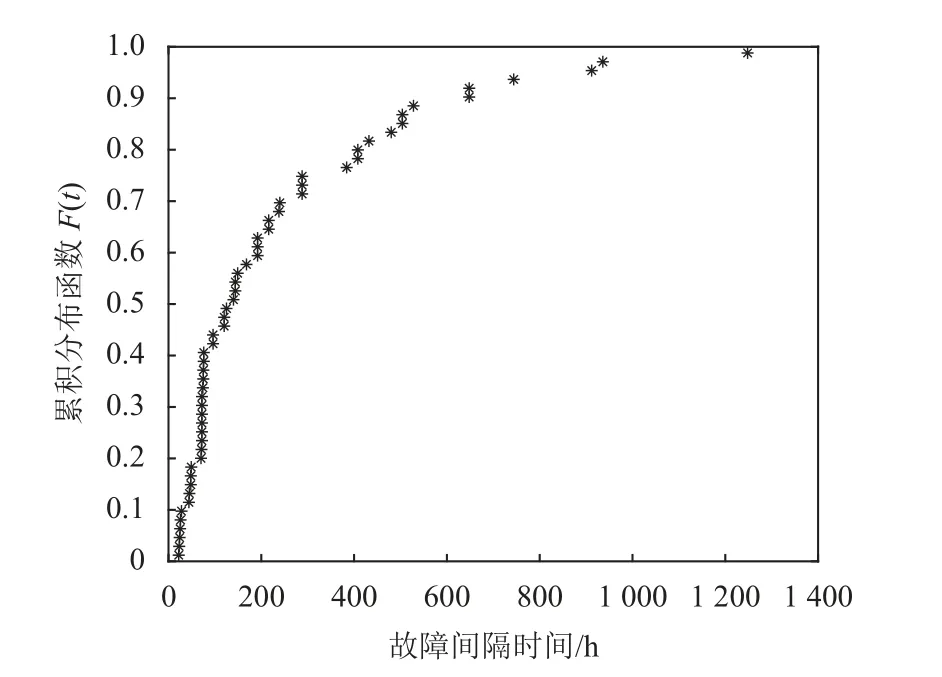
图2 样本的数据点分布图

将参数估计结果代入机床的可靠性模型，得到基于威布尔分布的机床拟合累计失效概率曲线，如图3 所示，图中虚线为95%置信区间的上下限。通过比较两条曲线的重合度来分析模型的拟合精度。

图3 最大似然估计下的威布尔模型分布函数

由图3 可知，通过极大似然估计得到的机床可靠性模型分布曲线，部分与参考数据点位重合，没有重合的部分也基本分布在置信区间内。

基于贝叶斯理论得到的参数估计结果如表2 所示，其中，用下标GBR 表示一般贝叶斯参数估计的结果，用下标HBR 表示分层贝叶斯参数估计的结果。

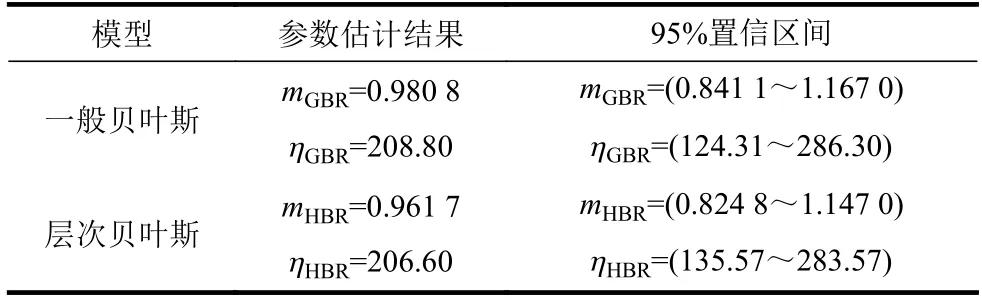
表2 一般贝叶斯和层次贝叶斯参数估计结果

通过对参数进行多层迭代，输入不同的初始值，构造马尔科夫链然后观察其抽样迭代过程是否收敛，运算迭代过程如图4、图5 所示。将α1=1,α2=200,β1=β2=0.5代 入 式(10)，α1=1,β1=0.5,α1′=α2′=0,β1′=100,β2′=1代入式(11)，得到待估参数的后验分布，如图6、图7 所示。

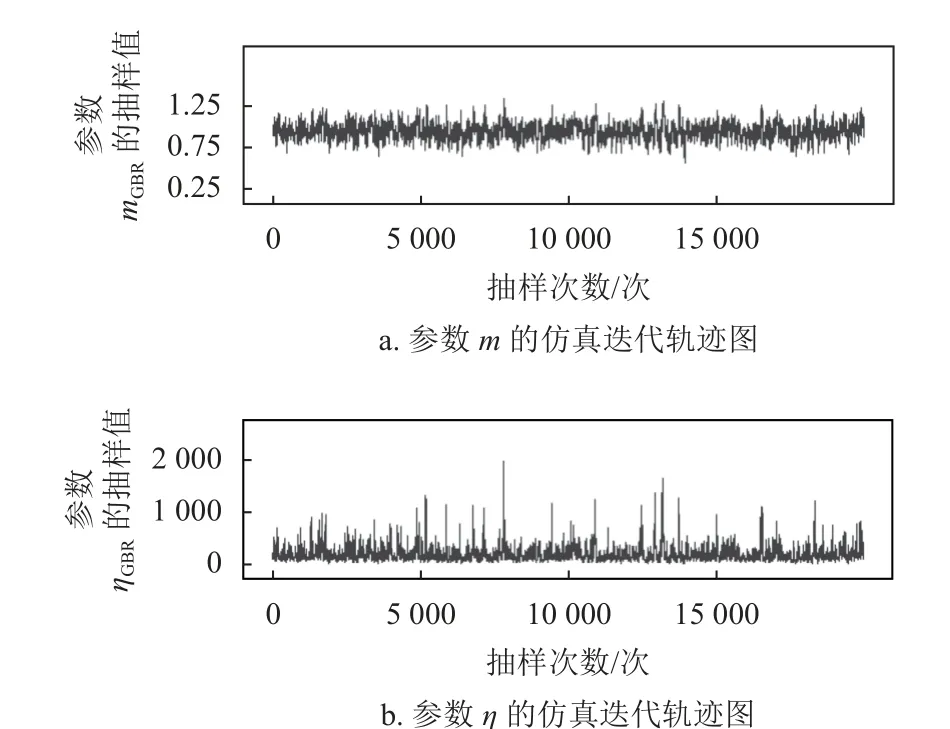
图4 基于一般贝叶斯模型的仿真迭代轨迹图

图5 基于分层贝叶斯模型的仿真迭代轨迹图

图6 基于一般贝叶斯模型的参数后验分布概率密度函数

图7 基于分层贝叶斯模型的参数后验分布概率密度函数

从待估参数的后验分布图中可以看出，分层贝叶斯参数估计的结果更加集中。将参数估计结果分别代入式(1)、式(13)中，得到图8、图9 所示的分布曲线。由此可知，贝叶斯模型与传统的模型相比，其拟合曲线与真实数据的重合度更高。

图8 一般贝叶斯估计下的曲线分布

图9 分层贝叶斯估计下的曲线分布

2.3 结果分析

将机床的3 种可靠性模型代入式(12)，计算得到NRMSE 值，结果分别为MLE=0.097 1，GBR=0.121 0，HBR=0.090 0。对比结果可知：分层贝叶斯模型相对于其他两个模型来说误差值更小，数据拟合效果更优；
基于极大似然估计法模型的NRMSE值低于一般贝叶斯模型的NRMSE 值。虽然此处传统可靠性模型精度比一般贝叶斯模型更优，可是随着经验信息的丰富，优化参数先验信息的设定后，可以逐渐改善参数估计的精确性。

2.4 不同样本量下的3 种参数估计方法对比

改变数据样本的容量，分别使用上述3 种参数估计方法，经过计算求出不同样本容量下的标准均方根误差值，结果如图10 所示。

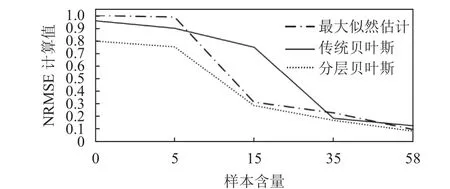
图10 不同样本量下的建模NRMSE 值

从图中可以看出，随着样本容量的增加，经过3 种参数估计方法得到的可靠性模型NRMSE 值均在下降，说明建模误差在降低，精度越来越好，当数据量趋于大数据样本时，贝叶斯方法依然有良好的可靠性。但当数据量较小时，其NRMSE 值更小，分层贝叶斯参数估计法有显著优势。特别是在样本量趋于0 时，基于极大似然估计建模得到的NRMSE 值近似于1，而基于贝叶斯理论建模得到NRMSE 值依然小于1，说明在样本量很小时，传统的方法几乎失去精确性，而基于贝叶斯理论得到的结果依然有效。综上所述，在数据量不足时，分层贝叶斯模型的拟合效果更优。

2.5 仿真验证

基于matlab 软件，将服从形状参数Beta=2 及尺度参数Eta=1 的双参数威布尔分布函数随机筛选10 组数据，把产生的小样本量代入到3 种参数估计方法中，得到表3 的结果。

表3 仿真估计结果对比

经过仿真分析也可以验证分层贝叶斯在进行小样本参数估计方面的优势，其估计的参数相对来说最接近真实值。

平均故障间隔时间(mean time between failures,MTBF)是常用的可靠性评价指标之一，是指产品从发生故障到下一次发生故障的平均工作时间，其表达式为：

式中，f(t)为概率密度函数。

将层次贝叶斯参数估计结果代入式(14)后，求得机床平均故障间隔时间为M TBF=210.215 h。分析可知，计算得到的MTBF 值小于所采集数据中的最大值1 248.000 h，210.215 h 大于所采集数据中的60%，经过排序分析处于中上位置。由此可见，平均故障间隔时间对于机床预防故障和维修保养有参考意义，说明了贝叶斯理论对于重型机床可靠性建模的有效性。

本文在重型数控机床故障数据小样本条件下，基于贝叶斯理论建立服从威布尔分布的可靠性模型，并对传统贝叶斯模型进行改进，得到分层贝叶斯模型。引入MCMC 算法求解贝叶斯模型的参数估计结果，对比极大似然估计法与贝叶斯参数估计的优劣，结果显示这两种参数估计结果近似，但贝叶斯参数估计法得到的参数置信区间更窄。采用NRMSE 分析参数估计结果精度，随着样本数据容量增大，传统参数估计法与贝叶斯参数估计法趋于一致，当数据样本较小时，分层贝叶斯模型得到的建模精度更高。对贝叶斯理论模型进行仿真实验，结果表明贝叶斯参数估计是有效的。利用贝叶斯可靠性模型对该重型数控机床进行可靠性评估，在机床故障数据小样本条件下，其评估结果更精确有效，对重型数控机床的可靠性研究有重要意义。

推荐访问:可靠性 数控机床 改进