唐 渐,刘玉清
(西南医科大学医学与信息工程学院,四川 泸州 646000)
在生物信息学的大力推动下,分子作为关键的活性物质[1],受到了物理、化学、生物、材料、计算机科学等多领域的高度关注,并逐渐演变为众多领域的热点话题。生物分子所具备的性质[2]不仅决定着国民的生命健康与安全,而且对生物自身的应用与发展有着极其深远的影响,因此,有必要研究出一种快速且易于实现的分子性质预测方法。
近几年,相关领域研究人员在分子性质预测方向取得了较好的成就。比如:谭露露等人[3]采用多特征融合图卷积方法,就分子的生物活性展开预测;
苏敏仪等人[4]应用应用机器学习方法,针对药物分子的解离速率常数,构建预测模型。尽管以上方法已经取得了较好的应用成果,但在预测的性质类别上存在一定局限性。
为了解决以上问题,本文以图神经网络为基本算法,提出分子性质预测方法。在数据处理任务中,以图神经网络[5]的表现最为突出,结合图数据与神经网络。作为深度神经网络的泛化形式,图神经网络现已广泛应用于生命科学、知识图谱等重大领域。对于本文研究成效而言,图神经网络依据与分子结构之间的依赖关系,为分子性质分析与预测提供了强大的建模助力,有助于加强模型预测性能;
卷积优化图神经网络能赋予分子结构图由浅至深的特征,聚合更新的内部传输机制使图卷积神经网络更具灵活性,通过加强节点间的信息聚合与传递,有助于提升不规则图数据的分子性质预测准度。
2.1 图神经网络
根据图形种类的顶点-边结构,构建(赋权)无向图[6]、(赋权)有向图[7]、循环图[8]等多种图类型数据,作为神经网络的输入项来获取输出结果,即图神经网络。假设任意类型图G的顶点集合是V,边集合是E,则图G的表示形式如下所示
G=(V,E)
(1)
其中,图G边的方向有无主要取决于顶点间的方向依赖关系;
图顶点即神经网络的节点。
已知节点v的特征xv关联于节点的真实标签,若想根据图G的部分标记节点,预测出未标记节点的标签,则采用下列表达式界定各网络节点
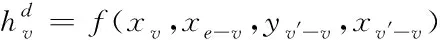
(2)



(3)



(4)
其中,g表示输出函数公式,即前馈全连接神经网络层。
2.2 图卷积神经网络
分子结构相对复杂,不规则数据较多,导致传统图神经网络无法处理图中的非规则数据与边缘信息,扰乱分子节点分布形式,影响节点间关系的精准描述。因此,利用傅里叶变换方法[11]在图神经网络中引入谱卷积,构建图卷积神经网络。
运用图拉普拉斯矩阵[12]的特征逆矩阵UT,通过下列表达式把输入节点v转换至傅里叶的域φ中

(5)
其中,逆矩阵UT已作归一化处理;
vφ表示傅里叶域中的输入节点;
N表示单位矩阵;
D、A分别指代度量矩阵与邻接矩阵。
利用下式卷积操作节点vφ与卷积核:
J=U·γ·UTvφ
(6)
式中,U表示图拉普拉斯矩阵的特征矩阵。
为降低卷积运算难度,采用下列切比雪夫多项式实现卷积操作,获取近似卷积结果

(7)
式中,λmax表示图拉普拉斯矩阵L的最大特征值。
实际的输出结果应是多维节点特征,而非一维项。因此结合邻接矩阵A与节点自身特征,通过下列表达式进行更新,得到多维的节点特征x′v
x′v=f(Xt,A)=sigmoid[(A+N)·Xt·ω(0)]
(8)
式里,sigmoid为激活函数[13];
ω(0)是网络层的连接权值。
将聚合、更新两阶段作为图卷积神经网络的内部传输机制,加强网络各节点间的信息聚合与传递,提高预测精准度。因此此传输机制下图卷积神经网络的分子性质预测流程如图1所示。
具体实现步骤描述如下:

图1 分子性质预测流程
1)融合分子结构图与图卷积神经网络:设定图G顶点v(即网络节点)为分子结构的原子,边为结构化学键,则图节点的特征xv即原子特征,包含原子的元素种类、度数、电荷量等多种特征;
图连边的特征xe-v即化学键特征,包含化学键的类型、位置、空间属性等特征。


(9)



(10)


(11)
4)预测分子性质:在反复的聚合与更新过程中,结合所有原子得到整个图G结构的表征形式,即分子结构向量G′,如下所示

(12)
将向量G′作为网络的待输入图类数据,则基于原子v的图卷积神经网络输出结果Y如下所示,即根据由原子特征与化学键特征构成的分子结构,得到的分子性质预测结果为

(13)
式中,Wt表示第t层的网络学习矩阵算法。

(14)
由此推导出下列损失函数Loss的界定公式
(15)
其中,Xe-v表示化学键特征xe-v的所有关联项。
为使各变量相对于图卷积神经网络参数均具备可微属性[15],利用激活函数sigmoid将上列损失函数Loss界定式改写成下列表达式

(16)
其中,η表示激活函数的修正系数。
4.1 数据集的选取与处理
从开源的GEO数据集[16]中选取含有十万以上不规则分子的子集。该子集中的分子属性种类及性质均值如表1所示。

表1 实验用数据集中分子相关信息
为避免子集中分子发生过拟合现象[18],归一化处理[19]所选数据集,降低分子性质的预测误差,提高训练效率。利用数据集80%的训练样本获取最优网络参数后,综合评价研究方法、文献[3]的基于特性融合图卷积方法的分子生物活性预测方法以及文献[4]的基于机器学习的分子性质预测方法的精准性、泛化性、迁移性等预测能力。
4.2 分子性质预测精度
不同分子属性种类的预测精度变化趋势如图2所示。
根据图2可以看出,本文针对复杂分子结构的不规则数据与边缘信息,利用傅里叶变换方法引入谱卷积而构建出的图卷积神经网络,使误差评估指标均值不超过0.15,决定系数始终位于0.999以上,能满足实际应用中的精准度需求。所得实验结论足以说明,该方法不仅在精准预测分子性质方面取得了出色的表现,而且对于大规模数据集具有较好的处理能力。

图2 预测精准性评价结果示意图
4.3 分子性质预测的泛化性分析
方法泛化性[20]的检测目的主要是验证预测方法对小数据集是否具备较强的学习能力。从实验用数据集中随机选取出四种不同规模的数据子集,利用本文方法对四个数据集分别展开分子性质预测,由均方根误差指标进行评估,分析模型的泛化性能。为突显本文方法的优越性,将基于特性融合图卷积方法的分子生物活性预测方法以及基于机器学习的分子性质预测方法作为对比项,不同方法的均方根误差数据变化趋势如图3所示。
由图3可知,各方法的均方根误差值均随着数据集规模的变小而增大;
两个对比方法的上升趋势近似于线性,增幅较大;
而本文的图卷积神经网络则依据聚合与更新的内部传输机制,通过加强各原子间的信息聚合与传递能力,有效抑制了均方根误差值的增加幅度,即便是50MB数据量的小规模数据集,指标值也没有超过0.25。

图3 预测模型泛化性评价结果示意图
4.4 分子性质预测的迁移性分析
方法迁移性的检测目的主要是验证预测方法是否能将从小规模数据集习得的知识应用于其它数据集上。以选取的50MB数据集作为学习样本,检验三种方法对整个实验用数据集的分子性质预测能力,各方法的评估指标数据变化趋势如图4所示。
对比大规模样本数据集的预测结果可知,本文方法的误差类指标值略有上升,决定系数指标值略有下降;
尽管学习样本数据量大幅减少,但相较于对比方法的高误差值、低拟合度,本文通过融合分子结构图、聚合邻域信息、更新原子结构等阶段,既实现了对原子特征的表示学习,也取得了整个图形数据的结构,因此误差指标均值仅有0.218,决定系数相对趋近于0.999,依旧具有较为优越的预测能力。

图4 预测模型迁移性评价结果示意图
在材料、药物、食品等领域中,多元化分子的性质与属性研究,对拓宽所属物料的应用前景、赋予更高的实践价值具有重要的指导作用。为探寻性能更优越的物料,准确预测出未知结构的分子性质是必要且重要的。随着人工智能领域飞速发展,利用计算机相关技术来处理大规模数据信息的手段已相对成熟。因此,本文尝试将人工智能技术中的神经网络与分子性质预测课题相结合,并取得了不错的成效。
为进一步推动人工智能技术与物料分子研究的融合深度与研究进程,为相应领域的候选物料提供更精准的分子结构参考依据,将以下几个方面作为今后深入探究的重点:选取的实验数据集相对单一,应就其它数据集展开仿真,检验方法的适用性;
分子结构分为同构与异构两种形式,应继续学习分子理论知识,从同构分子图与异构分子图角度,完善图神经网络算法;
应深入探索跨领域时分子的化学、物理、药理等属性对预测结果的影响,使预测任务更具针对性,扩大方法的应用范围。
