一种适应低信噪比的脉内识别算法

曹俊纺，张玉喜，吴 昊，臧 勤

(中国船舶集团有限公司第八研究院，南京 211153)

雷达信号脉内调制类型识别是现代雷达侦察设备的一项重要功能。常用的脉内特征分析方法普遍对信噪比有一定的要求，当信噪比过低时，无法完成调制类型识别。本文首先对雷达脉冲信号进行时间和脉宽格子划分，对同一格子中信号基于一阶差分自相关函数生成特征向量，聚类统计后再将分类后的每组信号进行平方处理，再次计算特征向量，完成对几种脉内调制类型脉冲分类。在分类基础上选取每组中部分质量较好的脉冲完成脉内调制类型识别，仿真结果证明该算法能够有效提高信号分类识别准确率。

1.1 算法原理

根据文献[1]、[2]，假设雷达侦察接收机接收的脉冲离散信号为

x(n)=s(n)+n(n), 1≤n≤N

(1)

式中，s(n)为雷达脉冲信号；
n(n)为高斯白噪声；
N为雷达脉冲信号的脉冲宽度。

一阶差分信号定义为

y(n)=x(n)-x(n-1),n=2,3,…,N

(2)

定义一阶差分信号的自相关函数为

Ry(k)=E{y*(n)y(n+k)}

=E{[x*(n)-x*(n-1)][x(n+k)-x(n+k-1)]}

=E{x*(n)x(n+k)-x*(n)x(n+k-1)-

x*(n-1)x(n+k)+x*(n-1)x(n+k-1)}

(3)

式中，k为时间延迟。

瞬时自相关定义为

Bx(n,k)=x*(n)x(n+k)

=[s*(n)+n*(n)][s(n+k)+n(n+k)]

=s*(n)s(n+k)+s*(n)n(n+k)+

n*(n)s(n+k)+n*(n)n(n+k)

(4)

式(4)中信号部分的瞬时自相关为

rs(n,k)=s*(n)s(n+k)

(5)

假定信号与噪声不相关，互相关值接近于0，噪声的自相关也接近于0，得到如下近似公式：

Bx(n,k)≈rs(n,k)

(6)

Ry(k)≈E{rs(n,k)-rs(n,k-1)-

rs(n-1,k+1)+rs(n-1,k)}

(7)

包络特征为

(8)

(9)

对一组个数为q的时延序列得到的平均距离J(k)进行降序排列，降序后对应的时延序列记作{d1,d2,…,dq}。根据文献[1]、[2]，对时延序列进行二次重排，时延序列为{D1,D2,…,Dq}。选取前3个时延，得到特征向量组V=[U(D1),U(D2),U(D3)]。

对获取的特征向量组V=[U(D1),U(D2),U(D3)]，根据不同脉内调制类型信号的特征向量范围制定相应门限，采用聚类方法对脉冲进行分类分组。

1.2 不同信噪比下不同脉内调制类型信号的特征向量分布

根据上述算法，对5种不同脉内调制类型信号进行仿真，每种调制信号50个样本。仿真参数如下：信号采样率为400 MHz，信号的初始相位为0。

(1) 简单信号(NS)：脉宽10 μs，载频150 MHz；

(2) 线性调频信号(LFM)：脉宽10 μs，起始频率100 MHz，终止频率150 MHz；

(3) 二相编码信号(BPSK)：脉宽14 μs，载频150 MHz，编码选择7位的Bark码；

(4) 四相编码信号(QPSK)：脉宽16 μs ，载频150 MHz，编码选择16位的Frank码；

(5) 频率编码信号(FSK)：脉宽10 μs，载频分别为100 MHz和150 MHz，编码采用5位随机码。

选择3个时延分别为k1=20，k2=100，k3=200，得到特征向量V=[U(20),U(100),U(200)]。图1为不同信噪比条件下仿真信号的特征向量分布。可以看出：当信噪比低至-5～0 dB时，调制类型信号特征向量值虽然有分散，但仍具有较好的可区分性，分类效果明显；
当信噪比为-10～-5 dB时，信号特征聚集性较差，相互之间有交叠，分类准确率降低。

图1 不同信噪比下不同脉内调制类型信号的特征向量分布

由仿真分析试验可知，一阶差分自相关函数特征参数提取算法在低信噪比条件下具有较高的信号调制类型分类能力。试验中还发现信噪比越低，特征向量变化越大、越分散。部分特征向量值相近的调制类型信号在高信噪比下具有可区分性，在低信噪比下由于特征向量变化大，容易出现特征向量交叠情况。

仿真分析两组二相编码信号和四相编码信号，在0 dB信噪比条件下，生成特征向量分布图和不同延迟下的特征分布均值图如图2、图3所示。

图2 第1组信号特征分布图

图3 第2组信号特征分布图

第1组仿真信号参数：

(1) BPSK：脉宽40 μs，载频150 MHz，码元序列为{ 1,1,1,0,0,1,0,1,0,1,1,1,0}；

(2) QPSK：脉宽43 μs ，载频150 MHz，码元序列为{0,0,0,0,0,1,2,3,0,2,0,2,0,3,2,1}。

第2组仿真信号参数：

(1) BPSK：脉宽20 μs，载频150 MHz，码元序列为{1,1,1,0,0,1,0,1,0,1,1,1,0}；

(2) QPSK：脉宽20 μs，载频150 MHz，码元序列为{1,0,2,3,0,2,0,1,1,0,3,2,1}。

可以看出，当信噪比为0 dB时，由于信噪比较低，两组BPSK和QPSK信号特征值分布分散交叠，造成不同延迟下的特征分布均值相近，通过特征值不能有效对两种信号进行类型分类。为此，提出对低信噪比下BPSK和QPSK信号的进一步分类识别方法。

BPSK信号的平方是单载频信号，该单载频信号的频率是BPSK信号载频的2倍。QPSK信号的平方是BPSK信号，该BPSK信号的载频、初相是QPSK信号的2倍，两者码元宽度一样。两种类型信号通过平方处理后依然能保留或获取到原信号的特征参数。因此，针对低信噪比下可能存在的特征值分布有交叠的BPSK和QPSK信号，采取对原始信号进行平方处理，然后再采用一阶差分自相关函数特征参数提取算法进行特征提取分类识别。

图4为两组BPSK和QPSK信号经过平方和一阶差分自相关函数特征参数提取后的特征分布图，可以看出经过平方处理后的特征值分布具有较好的聚集性，分类效果明显。

图4 两组信号平方后的特征分布图

实际接收的雷达信号会有多种脉冲调制类型、多种脉冲宽度、不同信噪比脉冲交织的情况，对信号进行分类识别时，如果对所有脉冲同时计算特征向量，会存在数据量大、特征向量值组容易交叠等问题。针对实际接收的雷达脉冲信号流特点，为避免特征值重叠，并提高处理速度及分类准确率，提出基于时间格子和脉宽格子的特征提取方法。根据脉冲到达时间先划分时间格子，可根据脉冲流密度和处理计算能力设置时间格子大小。对同一时间格子中的脉冲流进行脉宽格子划分，即根据脉冲脉宽大小划分格子，对同一脉宽格子内的脉冲依次进行特征向量提取和聚类统计分类。对分类后的每组信号进行信号平方后的二次特征向量提取，再次进行聚类处理，实现低信噪比下基于一阶差分自相关特征提取算法的信号分类。

脉冲信号处理流程如图5所示。雷达中频脉冲信号输入数据预处理模块，计算脉冲脉宽、到达时间等参数。根据脉冲到达时间划分时间格子，对每个时间格子内的脉冲划分脉宽格子。对每个脉宽格子中的脉冲采用一阶差分自相关函数特征向量提取算法来获取特征向量值，通过聚类算法实现脉冲流分类。对分类后的每组脉冲依次进行平方处理、特征值提取和聚类统计分类，二次计算可有效解决部分BPSK和QPSK信号可能存在的特征交叠问题。在分类后的脉冲组内选择部分质量较好的脉冲进行脉内特征自动识别[3-5]。在低信噪比情况下，信号的频谱特征具有较好的区分度，结合识别算法给出脉内调制类型识别结果。

图5 脉冲信号处理流程框图

在SNR为-4～5 dB条件下，对NM、LFM、BPSK、QPSK、FSK信号进行仿真，NM、LFM、FSK参数设置同1.2节，BPSK、QPSK参数设置同第2节中第2组，脉宽格子宽度为10 μs。特征向量计算中延迟值采用1.1节中的时延序列二次排序，选择最优算法计算获取3个最优延迟值，延迟范围为20～400采样点，步进为20采样点。计算每种调制类型信号对应延迟值的特征向量，采用聚类方法分类识别特征向量。

对上述5种信号进行仿真，每种信号500个样本，共2 500样本，对样本进行聚类分组。不同信噪比下各组样本脉冲聚类分类结果如表1所示。

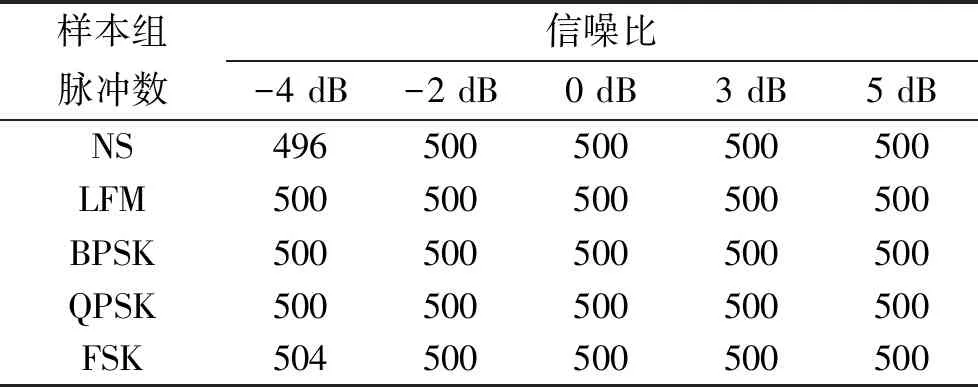
表1 各组类型脉冲聚类分类结果

可以看出，对仿真信号进行分析处理，在信噪比大于等于-4 dB时信号具有良好的分类效果。经过信号平方后再处理，BPSK和QPSK同样具有良好的分类结果。完成区域分类后，在每组脉冲数据中选取1个或多个信噪比高、质量较好的脉冲数据进行脉内调制类型识别，分析出该组数据的脉内调制类型，可以减少处理脉冲个数，有效提高处理速度。另外，由于脉内调制类型识别采用质量较好的脉冲，有效提高了识别准确率。

本文对雷达脉冲信号进行时间格子和脉宽格子划分，对同一格子中信号采用一阶差分自相关函数特征提取算法，生成相应的特征向量，根据特征向量进行聚类统计，对信号进行分类。对分类后的每组脉冲再通过采用平方后二次计算特征向量方式，实现对易混叠信号的信号类型分类。对分类后的每组脉冲，选择质量好的脉冲进行调制类型识别。仿真验证了算法在低信噪比条件下具有较好的分类识别性能。在实际工程应用中，可以基于该算法设计出相应分类识别模块，在实时性要求不高、低信噪比的环境下使用。

推荐访问:算法 识别 信噪比